Matched-Field Processing - Synthetic 2D case¶
The match-field processing performed in this code is inspired from the one describe in this git repository. The description below is taken from this repository.
The beamformer formulation is written in the frequency domain as:
where \(K_{jk}(\omega) = d_j(\omega) d_k^H(\omega)\) is the cross-spectral density matrix of the recorded signals \(d\), and \(S_{jk}(\omega) = s_j(\omega) s_k^H(\omega)\) is the cross-spectral density matrix of the synthetic signals \(s\).
Here, \(j\) and \(k\) identify sensors, and \(H\) denotes the complex conjugate. Auto-correlations (\(j = k\)) are excluded because they contain no phase information. Consequently, negative beam powers indicate anti-correlation.
The synthetic signals \(s\) (often called replica vectors or Green’s functions) represent the expected wavefield for a given source origin and medium velocity, most often in an acoustic homogeneous half-space \(s_j = \exp(-i \omega t_j)\) where \(t_j\) is the travel time from the source to each receiver \(j\).
The travel time is computed as:
with \(| \mathbf{r}_j - \mathbf{r}_s |\) being the Euclidean distance between the sensor and the source, and \(c\) the medium velocity.
Using this formulation the Bartlett \(B\) in contained in \([-1,1]\).
[ ]:
from itertools import product
import dask.array as da
import matplotlib.pyplot as plt
import numpy as np
import xarray as xr
import pylab as plt
import torch
from tqdm import tqdm
# specific das_ice function
import das_ice.io as di_io
import das_ice.signal.filter as di_filter
import das_ice.processes as di_p
import das_ice.plot as di_plt
import das_ice.mfp as di_mfp
# classic librairy
import torch
import xarray as xr
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
%matplotlib inline
[3]:
from dask.distributed import Client,LocalCluster
cluster = LocalCluster(n_workers=8)
client = Client(cluster)
client.dashboard_link
[3]:
'http://127.0.0.1:8787/status'
Defined captor position¶
In this exemple, 4 sensors are defined.
[4]:
nb_sensor=4
random_sensor=[]
for i in range(nb_sensor):
random_sensor.append([np.random.randint(-70, 71),np.random.randint(-70, 71),0])
sensors=np.array(random_sensor)
Generate signal¶
This section shows how to genrate signal that are similar to DAS data. Two events are compute.
[6]:
nb_sources=4
random_sources=[]
for i in range(nb_sources):
random_sources.append([np.random.randint(-70, 71),np.random.randint(-70, 71),0])
if i==0:
dart=di_mfp.artificial_sources_freq(sensors,random_sources[-1],2500,window_length=.1,sampling_rate=25000)
else:
dart2=di_mfp.artificial_sources_freq(sensors,random_sources[-1],2500,window_length=.1,sampling_rate=25000)
dart2['time']=dart2['time']+dart['time'][-1]+dart['time'][1]
dart=xr.concat([dart,3*dart2],'time')
plt.figure()
for i in range(dart.shape[0]):
dart[i,:].plot(label=i)
plt.legend()
plt.grid()
[7]:
dart2
[7]:
<xarray.DataArray (distance: 4, time: 2501)> Size: 80kB
array([[-0.00055941, 0.00055953, -0.00055946, ..., 0.00055629,
-0.00055744, 0.00055748],
[-0.00092802, 0.00093086, -0.00093362, ..., 0.0009191 ,
-0.00092211, 0.00092503],
[-0.00037042, 0.00037006, -0.00037069, ..., 0.00037012,
-0.0003703 , 0.00037064],
[-0.00064768, 0.00064872, -0.00064954, ..., 0.00064358,
-0.00064489, 0.00064615]], shape=(4, 2501))
Coordinates:
* time (time) float64 20kB 3.001e+08 3.002e+08 ... 4.001e+08 4.001e+08
Dimensions without coordinates: distancePerformed MFP¶
This MPF implementation if taken from the dask implementation from this git repository.
3D MFP¶
Example of 3D MFP.
[6]:
help(di_mfp.MFP_3D_series)
Help on function MFP_3D_series in module das_ice.mfp:
MFP_3D_series(ds, delta_t, stations, xrange=[-100, 100], yrange=[-100, 100], zrange=[-100, 100], vrange=[2500, 2500], freqrange=[100, 200], dx=5, dy=5, dz=5, dv=250, n_fft=None)
Perform Matched Field Processing (MFP) on 3D series data to compute beamforming power
over a range of spatial coordinates, velocities, and frequencies.
:param ds: Input data as an xarray DataArray containing waveform data.
Must include 'distance' and 'time' coordinates.
:type ds: xarray.DataArray
:param delta_t: Time window size (in seconds) for processing the data in small chunks.
:type delta_t: float
:param stations: List of station coordinates used for processing.
:type stations: list of tuples or ndarray of shape (n_stations, 3)
:param xrange: Range of horizontal x-coordinates to search (start and end), default is [-100, 100].
:type xrange: list of float or int
:param yrange: Range of horizontal y-coordinates to search (start and end), default is [-100, 100].
:type yrange: list of float or int
:param zrange: Range of depths to compute (start and end), default is [-100, 100].
:type zrange: list of float or int
:param vrange: Velocity range to search in m/s (start and end), default is [2500, 2500].
:type vrange: list of float or int
:param freqrange: Frequency range for processing in Hz (start and end), default is [100, 200].
:type freqrange: list of float
:param dx: Spacing between grid points in the horizontal x dimension, default is 5.
:type dx: float or int
:param dy: Spacing between grid points in the horizontal y dimension, default is 5.
:type dy: float or int
:param dz: Spacing between grid points in the depth dimension (z), default is 5.
:type dz: float or int
:param dv: Spacing between velocities, default is 250.
:type dv: float or int
:return: A 4D xarray DataArray containing the computed beampower values. The dimensions are
'velocity', 'true_time', 'x', 'y', 'z'.
:rtype: xarray.DataArray
[14]:
sensors.shape
[14]:
(4, 3)
[8]:
MFP3D=di_mfp.MFP_3D_series(dart,0.1,sensors,xrange=[-70,70],yrange=[-71,71],zrange=[0,0],dx=1,dy=1,dz=1,n_fft=None)
/home/chauvet/miniforge3/envs/taconaz2025/lib/python3.11/site-packages/distributed/client.py:3363: UserWarning: Sending large graph of size 13.55 MiB.
This may cause some slowdown.
Consider loading the data with Dask directly
or using futures or delayed objects to embed the data into the graph without repetition.
See also https://docs.dask.org/en/stable/best-practices.html#load-data-with-dask for more information.
warnings.warn(
Filename: /home/chauvet/Documents/Gitlab/das_ice/das_ice/mfp.py
Line # Mem usage Increment Occurrences Line Contents
=============================================================
114 778.8 MiB 778.8 MiB 1 @profile
115 def MFP_3D_series(ds,delta_t,stations,xrange=[-100,100],yrange=[-100,100],zrange=[-100,100],vrange=[2500,2500],freqrange=[100,200],dx=5,dy=5,dz=5,dv=250,n_fft=None):
116 '''
117 Perform Matched Field Processing (MFP) on 3D series data to compute beamforming power
118 over a range of spatial coordinates, velocities, and frequencies.
119
120 :param ds: Input data as an xarray DataArray containing waveform data.
121 Must include 'distance' and 'time' coordinates.
122 :type ds: xarray.DataArray
123
124 :param delta_t: Time window size (in seconds) for processing the data in small chunks.
125 :type delta_t: float
126
127 :param stations: List of station coordinates used for processing.
128 :type stations: list of tuples or ndarray of shape (n_stations, 3)
129
130 :param xrange: Range of horizontal x-coordinates to search (start and end), default is [-100, 100].
131 :type xrange: list of float or int
132
133 :param yrange: Range of horizontal y-coordinates to search (start and end), default is [-100, 100].
134 :type yrange: list of float or int
135
136 :param zrange: Range of depths to compute (start and end), default is [-100, 100].
137 :type zrange: list of float or int
138
139 :param vrange: Velocity range to search in m/s (start and end), default is [2500, 2500].
140 :type vrange: list of float or int
141
142 :param freqrange: Frequency range for processing in Hz (start and end), default is [100, 200].
143 :type freqrange: list of float
144
145 :param dx: Spacing between grid points in the horizontal x dimension, default is 5.
146 :type dx: float or int
147
148 :param dy: Spacing between grid points in the horizontal y dimension, default is 5.
149 :type dy: float or int
150
151 :param dz: Spacing between grid points in the depth dimension (z), default is 5.
152 :type dz: float or int
153
154 :param dv: Spacing between velocities, default is 250.
155 :type dv: float or int
156
157 :param n_fft: n in torch.fft.fft function
158 :type dv: int
159
160 :return: A 4D xarray DataArray containing the computed beampower values. The dimensions are
161 'velocity', 'true_time', 'x', 'y', 'z'.
162 :rtype: xarray.DataArray
163 '''
164
165 778.9 MiB 0.0 MiB 1 sampling_rate=(ds.time[1]-ds.time[0]).values.astype(float)*10**-9
166 # defined number of sample per time series
167 778.9 MiB 0.0 MiB 1 dn=int(delta_t/sampling_rate)
168 # build a data cube with a dimention for each time series
169 778.9 MiB 0.0 MiB 1 ll=[]
170 778.9 MiB 0.0 MiB 1 true_time=[]
171 778.9 MiB 0.0 MiB 1 din=int(len(ds.time)/dn)
172 778.9 MiB 0.0 MiB 5 for i in range(din):
173 778.9 MiB 0.0 MiB 4 tmp=ds[:,i*dn:(i+1)*dn]
174 778.9 MiB 0.0 MiB 4 new_time = np.arange(dn) * sampling_rate
175 778.9 MiB 0.0 MiB 4 true_time.append(tmp.time[0].values)
176 778.9 MiB 0.0 MiB 4 tmp = tmp.assign_coords(time=new_time)
177 778.9 MiB 0.0 MiB 4 ll.append(tmp)
178 778.9 MiB 0.0 MiB 1 ds_cube=xr.concat(ll,dim='true_time')
179 ############
180 ##
181 ############
182 778.9 MiB 0.0 MiB 1 if n_fft is None:
183 778.9 MiB 0.0 MiB 1 n_fft=len(ds_cube.time)
184 else:
185 sampling_rate*=len(ds_cube.time)/n_fft
186
187
188 # Fiber signal processing
189 779.8 MiB 0.9 MiB 1 multi_waveform_spectra=torch.fft.fft(torch.from_numpy(ds_cube.values),axis=2,n=n_fft).to(dtype=torch.complex128)
190 779.8 MiB 0.0 MiB 1 freqs = torch.fft.fftfreq(n_fft,sampling_rate)
191 # Normalized over each frequencies
192 780.4 MiB 0.5 MiB 1 spectral_norm = torch.abs(multi_waveform_spectra) # Spectral norm
193 # Replace 0 values with 1
194 781.3 MiB 0.9 MiB 1 spectral_norm[spectral_norm == 0] = 1
195 781.9 MiB 0.7 MiB 1 multi_waveform_spectra = multi_waveform_spectra/spectral_norm
196 #
197 781.9 MiB 0.0 MiB 1 omega = 2 * torch.pi * freqs
198 # frequency sampling
199 782.2 MiB 0.3 MiB 1 freq_idx = torch.where((freqs >= freqrange[0]) & (freqs <= freqrange[1]))[0]
200 782.3 MiB 0.1 MiB 1 omega_lim = omega[freq_idx]
201 782.4 MiB 0.1 MiB 1 waveform_spectra_lim = multi_waveform_spectra[:,:,freq_idx]
202
203
204
205 782.6 MiB 0.2 MiB 1 K = waveform_spectra_lim[:,:, None, :] * waveform_spectra_lim.conj()[:,None, :, :]
206 782.6 MiB 0.1 MiB 1 diag_idxs = torch.arange(K.shape[1])
207 782.8 MiB 0.2 MiB 1 zero_spectra = torch.zeros(omega_lim.shape, dtype=torch.cdouble)
208 782.9 MiB 0.1 MiB 1 K[:,diag_idxs, diag_idxs, :] = zero_spectra
209 782.9 MiB 0.0 MiB 1 K = da.from_array(K.numpy())
210
211 # Compute grid
212 782.9 MiB 0.0 MiB 1 x_coords = torch.arange(xrange[0], xrange[1] + dx, dx)
213 782.9 MiB 0.0 MiB 1 y_coords = torch.arange(yrange[0], yrange[1] + dy, dy)
214 782.9 MiB 0.0 MiB 1 z_coords = torch.arange(zrange[0], zrange[1] + dz, dz)
215 782.9 MiB 0.0 MiB 1 v_coords=torch.arange(vrange[0], vrange[1] + dv, dv)
216 783.8 MiB 0.8 MiB 1 gridpoints = torch.tensor(list(product(x_coords, y_coords, z_coords)))
217
218 783.8 MiB 0.0 MiB 1 stations=torch.tensor(stations).to(dtype=torch.complex128)
219 783.8 MiB 0.1 MiB 1 distances_to_all_gridpoints = torch.linalg.norm(gridpoints[:, None, :] - stations[None, :, :], axis=2)
220
221 # Compute traveltimes
222 783.8 MiB 0.0 MiB 1 traveltimes=distances_to_all_gridpoints[None,:,:]/v_coords[:,None,None]
223 797.4 MiB 13.5 MiB 1 greens_functions = torch.exp(-1j * omega_lim[None, None,None, :] * traveltimes[:, :, :, None])
224 # move critical part to dask
225 810.9 MiB 13.5 MiB 1 greens_functions_dask = da.from_array(greens_functions.numpy(), chunks='auto')
226 810.9 MiB 0.0 MiB 1 S = (greens_functions_dask[:, :,:, None,:]*greens_functions_dask.conj()[:,:, None, :,:])
227 # Perform the einsum operation
228 810.9 MiB 0.0 MiB 1 beampowers_d = da.einsum("vlgijw, ljiw -> vlg", S[:, None , :, :, :, :], K).real
229 824.5 MiB 13.6 MiB 1 beampowers = beampowers_d.compute()
230 824.5 MiB 0.0 MiB 1 bp = beampowers.reshape(len(v_coords),din, len(x_coords), len(y_coords), len(z_coords))
231
232 824.5 MiB 0.0 MiB 1 res=xr.DataArray(bp,dims=['velocity','true_time','x','y','z'])
233 824.5 MiB 0.0 MiB 1 res['velocity']=v_coords
234 824.5 MiB 0.0 MiB 1 res['true_time']=true_time
235 824.5 MiB 0.0 MiB 1 res['x']=x_coords
236 824.5 MiB 0.0 MiB 1 res['y']=y_coords
237 824.5 MiB 0.0 MiB 1 res['z']=z_coords
238
239 824.5 MiB 0.0 MiB 1 res=res.transpose("x","y","z","velocity","true_time")/((stations.shape[0]-1)*stations.shape[0]*len(omega_lim))
240
241 824.5 MiB 0.0 MiB 1 return res
Show results¶
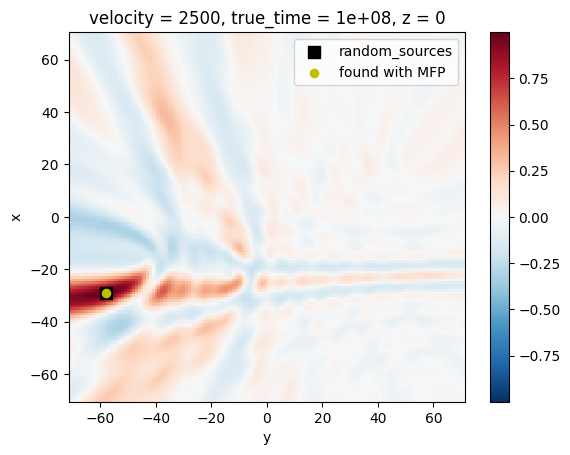
The MFP is finding the best match for:
[13]:
i_event=1
find_sources=MFP3D[...,i_event].where(MFP3D[...,i_event] == MFP3D[...,i_event].max(), drop=True).coords
find_sources
[13]:
Coordinates:
* velocity (velocity) int64 8B 2500
true_time float64 8B 1e+08
* x (x) int64 8B -29
* y (y) int64 8B -58
* z (z) int64 8B 0
The true sources was in:
[14]:
matching_index = np.where(MFP3D.z.values == find_sources['z'].values)[0]
MFP3D[...,matching_index,0,i_event].plot()
plt.scatter(random_sources[i_event][1],random_sources[i_event][0],s=80,marker='s',color='k',label='random_sources')
plt.scatter(find_sources['y'],find_sources['x'],s=35,color='y',label='found with MFP')
plt.legend()
[14]:
<matplotlib.legend.Legend at 0x7709f8160610>
3D plot of the MFP Bartlett with a slider to plot the different plane of the Bartlett field.